
- “A unifying feature among these systems is the use of cascading factors in multiplicative models to estimate outcomes.”
- “All systems incorporate probabilistic approaches to account for uncertainties.”
- “Sensitivity analysis identifies which parameters most significantly affect outcomes, guiding resource allocation and policy decisions.”
- “Many systems use hierarchical structures or networks to represent interactions.”
- “Differential equations model the dynamic changes in systems.”
- “Understanding and quantifying uncertainties allow for better risk management and decision-making.”
Table of Contents: (Click any link below to navigate to that section.)
- List fields of exploration similar to the Drake Equation in which there are cascading interdependent factors.
- Provide a robust, comprehensive mathematical formulation of the dynamics for each field.
- —— 1 —— The Seager Equation
- —— 2 —— Introduction to Epidemiological Modeling
- Basic Reproduction Number (R₀)
- Compartmental Models
- Basic Reproduction Number in the SIR Model
- Threshold Behavior
- SEIR Model
- Chain Binomial Models
- Stochastic Modeling
- Next-Generation Matrix
- Epidemic Modeling with Age Structure
- Network Models
- Metapopulation Models
- Control Measures
- Incorporating Cascading Factors
- Parameter Estimation
- Sensitivity Analysis
- Uncertainty Quantification
- Conclusion
- —— 3 —— Introduction to Risk Assessment and Reliability Engineering
- Reliability Theory
- Series and Parallel Systems
- Fault Tree Analysis (FTA)
- Minimal Cut Sets
- Reliability Block Diagrams (RBD)
- Probabilistic Risk Assessment (PRA)
- Bayesian Networks
- Markov Models
- Importance Measures
- Uncertainty Analysis
- Reliability Growth Modeling
- Common Cause Failures
- Life Data Analysis
- System Availability
- Failure Modes and Effects Analysis (FMEA)
- Incorporating Cascading Factors
- Sensitivity Analysis
- Bayesian Reliability Analysis
- Conclusion
- —— 4 —— Introduction to Conservation Biology and Ecology
- Population Growth Models
- Stochastic Population Models
- Metapopulation Dynamics
- Population Viability Analysis (PVA)
- Extinction Risk Models
- Genetic Diversity and Inbreeding
- Incorporating Environmental Variability
- Incorporating Catastrophes
- Sensitivity and Elasticity Analysis
- Harvesting and Conservation Strategies
- Allee Effects
- Incorporating Habitat Loss and Fragmentation
- Population Extinction Time Estimation
- Conclusion
- —— 5 —— Climate Science: Mathematical Formulation of Carbon Footprint Calculations and Global Warming Potential
- —— 6 —— Supply Chain and Project Management: Mathematical Formulation of PERT and Supply Chain Risk Models
- —— 7 —— Security and Defense Analysis: Mathematical Formulation of Kill Chain Models and Terrorism Risk Assessment
- —— 8 —— Public Health Policy: Mathematical Formulation of Health Impact Assessments and Multi-Criteria Decision Analysis
- —— 9 —— Environmental Impact Studies: Mathematical Formulation of Life Cycle Assessment and Cumulative Risk Assessment
- —— 10 —— Financial Risk Modeling and Portfolio Optimization: Mathematical Formulation of Market Dynamics and Risk Analysis
- Write an essay on the commonalities among these ten complex systems and the cross-domain insights.
- Quiz
- Provide 25 discussion questions relevant to the content above.

List fields of exploration similar to the Drake Equation in which there are cascading interdependent factors.
Fields that utilize cascading models similar to the Drake Equation—where a final estimate results from multiplying several factors, each with its own uncertainties or credences—span across various disciplines. Below is a list of such fields and corresponding models:
- Astrobiology and Exoplanet Studies:
- The Seager Equation: Developed by astronomer Sara Seager, this equation estimates the number of habitable planets with detectable biosignature gases. It multiplies factors like the number of stars observed, fraction with planets, planets in the habitable zone, planets with detectable biosignatures, etc.
- Rare Earth Hypothesis Factors: This approach considers the multitude of factors that make Earth suitable for complex life (e.g., right type of star, planetary mass, plate tectonics) and multiplies their probabilities to estimate the rarity of such planets.
- Epidemiology:
- Basic Reproduction Number (R₀): Calculated by multiplying factors like the contact rate, transmission probability per contact, and duration of infectiousness to estimate how contagious an infectious disease is.
- Chain Binomial Models: These models predict the spread of infectious diseases by considering probabilities of transmission through a series of contacts.
- Risk Assessment and Reliability Engineering:
- Fault Tree Analysis (FTA): A top-down approach that uses Boolean logic to combine probabilities of various subsystems failing, estimating the overall probability of system failure.
- Probabilistic Risk Assessment (PRA): Used in nuclear safety, aerospace, and other high-stakes industries to calculate the likelihood of catastrophic events by multiplying the probabilities of sequential failures or errors.
- Conservation Biology and Ecology:
- Species Extinction Risk Models: Estimate extinction probabilities by multiplying factors such as habitat loss rate, reproductive rate, genetic diversity, and environmental variability.
- Population Viability Analysis (PVA): Projects future population trends by considering birth rates, death rates, and other demographic factors.
- Climate Science:
- Carbon Footprint Calculations: Aggregate the emissions from various activities (transportation, energy use, manufacturing) by multiplying activity data by emission factors.
- Global Warming Potential (GWP): Estimates the impact of different greenhouse gases by considering their radiative forcing and atmospheric lifetime.
- Supply Chain and Project Management:
- PERT (Program Evaluation and Review Technique): Uses optimistic, pessimistic, and most likely estimates of task durations to calculate expected project timelines and probabilities.
- Supply Chain Risk Models: Assess the risk of supply chain disruptions by multiplying probabilities of failure at different stages (supplier reliability, transportation risks, demand variability).
- Security and Defense Analysis:
- Kill Chain Models: In military strategy, the success of a mission is determined by multiplying the probabilities of success at each stage (detection, identification, engagement).
- Terrorism Risk Assessment: Estimates the likelihood of a successful attack by considering factors like threat intent, capability, vulnerability of targets, and defenses.
- Public Health Policy:
- Health Impact Assessments (HIA): Evaluate the potential health effects of a policy or project by considering exposure levels, dose-response relationships, and population sensitivities.
- Multi-Criteria Decision Analysis (MCDA): Weighs various health outcomes by multiplying their probabilities and impacts to inform policy decisions.
- Environmental Impact Studies:
- Life Cycle Assessment (LCA): Calculates the environmental impacts of a product or service by summing the impacts across all stages, each quantified by multiplying activity data by impact factors.
- Cumulative Risk Assessment: Considers combined risks from multiple environmental stressors by integrating their individual probabilities and effects.
- Economic Forecasting:
- Input-Output Models: Estimate economic outcomes by multiplying sectoral inputs and outputs, considering factors like production coefficients and consumption rates.
- Cost-Benefit Analysis under Uncertainty: Multiplies the probabilities of different scenarios with their associated costs and benefits to determine expected values.
These models share the common feature of breaking down complex phenomena into a series of factors or events, each with its own probability or rate. By multiplying these factors, researchers and analysts can estimate the overall likelihood or magnitude of the event or outcome of interest, despite inherent uncertainties in each component.
Provide a robust, comprehensive mathematical formulation of the dynamics for each field.
—— 1 ——
The Seager Equation
The Seager Equation, proposed by astronomer Sara Seager, estimates the number of planets with detectable biosignature gases. It is formulated as:
Where:
: Number of planets with detectable signs of life.
: Number of stars observed.
: Fraction of quiet stars (suitable for observation).
: Fraction with planets in the habitable zone.
: Fraction of observable planets (e.g., those that transit their star).
: Fraction of planets that have life.
: Fraction where life produces detectable biosignatures.
Explanation of Each Factor:
Number of Stars Observed (): Total number of stars within the observational scope of a survey.*
Fraction of Quiet Stars (): Stars with low stellar activity, minimizing interference with observations.
Fraction with Planets in the Habitable Zone (): Probability that a quiet star hosts planets where conditions could support liquid water.
Fraction of Observable Planets (): Likelihood that planetary alignments allow for detection methods like transits.
Fraction with Life (): Probability that life arises on a habitable planet.
Fraction with Detectable Biosignatures (): Probability that life produces gases or signals we can detect.
Mathematical Formulation of Each Factor
1. Number of Stars Observed ( )
)
: Total number of stars in the galaxy or a specific region.
: Fraction covered by the survey or observational mission.
2. Fraction of Quiet Stars ( )
)
: Number of stars with low stellar activity.
: Total number of stars observed.
3. Fraction with Planets in the Habitable Zone ( )
)
This can be modeled using the planet occurrence rate:
: Planet radius.
: Semi-major axis (distance from the star).
: Planet occurrence rate density function.
: Inner and outer edges of the habitable zone.
4. Fraction of Observable Planets ( )
)
For the transit method:
: Stellar radius.
: Planetary radius.
: Semi-major axis.
Average Transit Probability:
Assuming :
5. Fraction with Life ( )
)
This is largely uncertain and often considered a constant or probability distribution based on hypothetical models:
6. Fraction with Detectable Biosignatures ( )
)
Depends on:
- Metabolic processes of life forms.
- Atmospheric accumulation of biosignature gases.
- Instrument sensitivity.
Incorporating Statistical Uncertainties
Each factor has associated uncertainties. To account for this, we can treat each factor as a random variable with a probability distribution.
Monte Carlo Simulation
We can perform simulations by sampling from the distributions of each factor:
- For each simulation run, draw values from the distributions of each
.
- Calculate
for each run.
- Aggregate results to obtain a probability distribution for
.
Example Distributions
- Uniform Distribution: When we have a range but no preferred value.
Beta Distribution: When values are between 0 and 1 with a shape defined by parameters and
.
Extended Models
Rare Earth Equation
The Rare Earth Equation estimates the number of Earth-like planets with complex life forms:
Where:
: Fraction of stars in the galactic habitable zone.
: Fraction of stars with planets.
: Number of habitable planets per system.
: Fraction where life arises.
: Fraction where complex life evolves.
: Fraction with a large moon.
: Fraction with Jupiter-like planets.
: Fraction with few extinction events.
Factors Explained:
- Galactic Habitable Zone (
): Region in the galaxy with favorable conditions.
- Large Moon (
): Stabilizes planetary tilt, affecting climate stability.
- Jupiter-like Planets (
): Gas giants that shield inner planets from excessive impacts.
Detection Probability Models
Transit Detection Probability ( )
)
For small planets around large stars, the probability decreases.
Radial Velocity Detection Probability
Depends on the radial velocity semi-amplitude:
: Radial velocity semi-amplitude.
: Gravitational constant.
: Orbital period.
: Planet mass.
: Stellar mass.
: Orbital inclination.
Detection requires above the instrument’s sensitivity threshold.
Advanced Statistical Modeling
Bayesian Framework
Allows updating probabilities with new data.
Posterior Probability:
: Model parameters.
: Observational data.
Likelihood Functions
Used to compare models or estimate parameters.
Maximizing gives the best-fit parameters.
Applications and Dynamics
- Planet Occurrence Rates: Statistical studies from missions like Kepler provide data on
.
- Stellar Activity: Impacts
and influences detection capabilities.
- Technological Advances: Improvements in telescopes and instruments affect
and
.
- Astrobiological Factors: Understanding of life’s adaptability influences
and
.
Combining Factors into a Comprehensive Model
- Each
represents a factor with its own dependencies and uncertainties.
- The product of all
factors determines the overall probability.
Key Dynamics:
- Multiplicative Effects: Small uncertainties in factors can lead to large variances in
.
- Interdependencies: Some factors may be correlated (e.g.,
and
).
- Temporal Changes: Galactic and planetary conditions evolve over time, affecting factors.
Conclusion
The mathematical formulation of astrobiology and exoplanet studies involves complex models that account for various astrophysical, biological, and technological factors. These models are crucial for estimating the prevalence of life-supporting planets and guiding future observational missions. By using probabilistic and statistical methods, scientists can better understand the uncertainties and refine these estimates as new data become available.
—— 2 ——
Introduction to Epidemiological Modeling
Epidemiological models are mathematical representations of how infectious diseases spread within populations. These models help in understanding the dynamics of disease transmission and in designing effective control strategies. Key models include:
- Compartmental Models: Divide the population into compartments based on disease status.
- Chain Binomial Models: Consider transmission probabilities through discrete contacts.
- Stochastic Models: Incorporate randomness inherent in disease spread.
Basic Reproduction Number (R₀)
The Basic Reproduction Number, denoted as , is a fundamental concept in epidemiology. It represents the average number of secondary infections produced by a single infected individual in a completely susceptible population.
Mathematical Definition
Where:
: Transmission rate (per capita rate at which an infected individual infects susceptible individuals).
: Duration of infectiousness.
Alternatively, can be expressed as:
Where:
: Contact rate (average number of contacts per individual per unit time).
: Probability of transmission per contact.
Explanation of Each Factor:
- Contact Rate (
): The average number of contacts an individual has per unit time that are sufficient for transmission.
- Transmission Probability (
): The probability that a contact between a susceptible and an infectious individual results in transmission.
- Duration of Infectiousness (
): The average period during which an infected individual can transmit the disease.
Compartmental Models
SIR Model
The SIR Model divides the population into three compartments:
- Susceptible (
): Individuals who can contract the disease.
- Infectious (
): Individuals who have the disease and can transmit it.
- Recovered (
): Individuals who have recovered and are immune.
Differential Equations
The dynamics are described by the following set of ordinary differential equations (ODEs):
Susceptible Population Dynamics:
Infectious Population Dynamics:
Recovered Population Dynamics:
Where:
: Total population size.
: Effective contact rate (transmission rate).
: Recovery rate (
).
Key Parameters:
Transmission Rate (): Combines contact rate and transmission probability.
Recovery Rate (): The rate at which infectious individuals recover.
Basic Reproduction Number in the SIR Model
Within the SIR framework, is calculated as:
This represents the expected number of secondary cases produced by a single infection in a fully susceptible population.
Threshold Behavior
- Disease Outbreak Condition: An outbreak will occur if
.
- Herd Immunity Threshold (
): The fraction of the population that must be immune to prevent an outbreak.
SEIR Model
The SEIR Model adds an Exposed () compartment for individuals who have been infected but are not yet infectious.
Differential Equations
Susceptible:
Exposed:
Infectious:
Recovered:
Where:
: Rate at which exposed individuals become infectious (
).
Chain Binomial Models
Chain binomial models simulate disease spread in discrete time intervals, considering the probabilistic nature of transmission.
Reed-Frost Model
Assumes:
- Fixed population size.
- Homogeneous mixing.
- No births, deaths, or recoveries during each interval.
Model Equations
Number of New Cases at Time :
Updating Susceptibles:
Where:
: Number of susceptibles at time
.
: Number of infectious individuals at time
.
: Probability of not transmitting the disease during a contact.
Transmission Probability:
Stochastic Modeling
Incorporates randomness to account for:
- Demographic Stochasticity: Randomness due to discrete individuals.
- Environmental Stochasticity: Randomness due to environmental fluctuations.
Master Equation
Describes the probability of being in a particular state at time
.
Due to complexity, often simulated using:
- Gillespie Algorithm: A Monte Carlo simulation method for stochastic processes.
Next-Generation Matrix
Used for more complex models to compute .
Construction
- Define Infected Compartments:
- Calculate Matrices:
- New Infections Matrix (
):
- New Infections Matrix (
Transition Matrix ():
Next-Generation Matrix ():
Basic Reproduction Number:
Where is the spectral radius (dominant eigenvalue) of
.
Epidemic Modeling with Age Structure
Incorporates age-dependent contact patterns.
Model Equations
Where:
: Susceptible individuals of age
at time
.
: Age-specific susceptibility.
: Contact rate between individuals of age
and
.
- Similar equations for
and
.
Network Models
Consider the population as a network where nodes represent individuals and edges represent contacts.
Probability of Infection Transmission
Where:
: Set of infectious neighbors.
: Probability of transmission from neighbor
.
Metapopulation Models
Divide the population into subpopulations connected by movement.
Model Equations
Where:
: Infectious individuals in subpopulation
.
: Movement rate from
to
.
Control Measures
Vaccination
Reduces the susceptible population.
Where is the vaccination coverage.
Quarantine and Isolation
Reduces contact rates.
Where is the fraction of contacts prevented.
Incorporating Cascading Factors
Each parameter can be broken down into sub-factors.
Transmission Rate ( )
)
Where:
: Base contact rate due to social behavior.
: Fraction accounting for compliance with social distancing.
: Base probability of transmission per contact.
: Environmental factors affecting transmission (e.g., humidity, temperature).
Parameter Estimation
Data Fitting
Use epidemiological data to estimate parameters via:
- Least Squares Method
- Maximum Likelihood Estimation
- Bayesian Inference
Example: Estimating  and
and 
Minimize the difference between model predictions and observed data:
Sensitivity Analysis
Assess how changes in parameters affect the model outcomes.
Basic Steps
- Select Parameters: Identify key parameters (
).
- Perturb Parameters: Vary each parameter within a plausible range.
- Analyze Outcomes: Observe changes in:
- Peak infection
- Total infected
- Duration of epidemic
- Peak infection
- Compute Sensitivity Indices:
Where is a parameter.
Uncertainty Quantification
Use probabilistic methods to account for uncertainties in parameters.
Monte Carlo Simulation
- Assign Distributions: For each parameter (
), define probability distributions.
- Sampling: Generate random samples of parameters.
- Simulation: Run the model for each sample set.
- Aggregate Results: Obtain confidence intervals for model outputs.
Conclusion
Epidemiological models are essential tools for understanding disease dynamics. By mathematically formulating the cascading factors—such as contact rates, transmission probabilities, and durations of infectiousness—we can predict outbreaks, evaluate control strategies, and inform public health policies. Incorporating uncertainties and conducting sensitivity analyses enhance the robustness of these models, making them invaluable in managing infectious diseases.
—— 3 ——
Introduction to Risk Assessment and Reliability Engineering
Risk Assessment and Reliability Engineering involve the application of mathematical methods to predict and analyze the reliability of systems and to assess the risks associated with system failures. These fields utilize probabilistic models to evaluate the likelihood of failures and their consequences.
Key concepts include:
- Reliability: The probability that a system performs its intended function without failure over a specified period under stated conditions.
- Risk: The combination of the probability of an event and its consequences.
- Fault Tree Analysis (FTA): A top-down approach that uses Boolean logic to model the pathways to system failures.
- Probabilistic Risk Assessment (PRA): A systematic and comprehensive methodology to evaluate risks associated with complex technological systems.
Reliability Theory
Basic Definitions
Reliability Function (): The probability that a system or component functions without failure up to time
.
Where is a random variable representing the time to failure.
Failure Probability (): The probability that a system fails by time
.
Failure Rate (): The instantaneous rate of failure at time
, given survival up to time
.
Where is the probability density function (PDF) of
.
Hazard Function (): Another term for the failure rate.
Series and Parallel Systems
Series Systems
In a series system, all components must function for the system to function.
System Reliability ():
Where is the reliability of component
.
Failure Probability:
Parallel Systems
In a parallel system, the system functions if at least one component functions.
System Reliability ():
Failure Probability:
Fault Tree Analysis (FTA)
Basic Concepts
- Top Event: The undesired event we aim to analyze.
- Intermediate Events: Events that occur due to the combination of basic events.
- Basic Events: The root causes or component failures.
- Logic Gates: Used to model the relationships between events.
- AND Gate: The output event occurs if all input events occur.
- OR Gate: The output event occurs if at least one input event occurs.
Boolean Expressions
For a fault tree, we can represent the top event using Boolean algebra. Let ,
,
, etc., represent basic events.
AND Gate:
The probability of :
(assuming independence)
OR Gate:
The probability of :
(assuming independence)
Fault Tree Construction
- Identify the Top Event: The system failure to be analyzed.
- Determine Contributing Events: Break down the top event into immediate causes.
- Use Logic Gates: Model the relationships between events using AND and OR gates.
- Quantify Basic Event Probabilities: Assign failure probabilities to basic events.
- Calculate the Top Event Probability: Use Boolean algebra and probability rules to compute the probability of the top event.
Example Calculation
Consider a system with three components ,
, and
. The top event occurs if either:
- Both
and
fail (AND gate).
- Or
fails (OR gate).
Boolean Expression:
Probability Calculation:
- Calculate
:
(assuming independence)
- Calculate
:
Minimal Cut Sets
- Cut Set: A set of basic events whose simultaneous occurrence leads to the top event.
- Minimal Cut Set: The smallest combination of basic events that cause the top event.
Calculating Top Event Probability Using Minimal Cut Sets
For small probabilities, we can approximate:
Reliability Block Diagrams (RBD)
An alternative to FTA, RBDs represent the system components in series and parallel configurations.
- Series Configuration: Components in series multiply their reliabilities.
- Parallel Configuration: Components in parallel have combined reliability as:
Probabilistic Risk Assessment (PRA)
PRA evaluates the risk of complex systems by considering sequences of events.
Event Trees
- Start from an initiating event and map possible sequences of successes and failures.
- Event Tree Analysis (ETA):
- Identify Initiating Events.
- Define Safety Functions or Systems.
- Develop Event Tree Paths.
- Assign Probabilities to Branches.
- Calculate Outcome Probabilities.
Risk Calculation
- Risk (
):
Where:
: Probability of scenario
.
: Consequence of scenario
.
Bayesian Networks
- Bayesian Networks: Probabilistic graphical models representing variables and their conditional dependencies.
- Useful for modeling complex systems with dependencies.
- Joint Probability Distribution:
Markov Models
- Used for systems with components that have multiple states and transitions.
- State Transition Diagram: Represents possible states and transitions.
- Transition Rate Matrix (
):
Where is the state probability vector.
Importance Measures
- Birnbaum’s Measure:
Indicates the sensitivity of the system reliability to component .
Uncertainty Analysis
Parameters often have uncertainties.
Monte Carlo Simulation
- Assign Probability Distributions: For component reliabilities
.
- Sampling: Generate random samples of
.
- Simulation: Calculate system reliability for each sample.
- Aggregate Results: Obtain the distribution of the system reliability.
Reliability Growth Modeling
Models that account for improvements over time due to fixes and redesigns.
- Crow-AMSAA Model:
Where:
: Failure rate at time
.
,
: Model parameters.
Common Cause Failures
Failures that affect multiple components simultaneously.
- Beta Factor Model:
: Fraction of failure rate due to common cause.
- Effective Failure Rate:
Life Data Analysis
- Weibull Distribution:
- Reliability Function:
Where:
: Scale parameter.
: Shape parameter.
System Availability
- Availability (
): The probability that a system is operational at a given time.
Where:
- Mean Time Between Failures (MTBF):
- Mean Time To Repair (MTTR): Average time to repair the system.
Failure Modes and Effects Analysis (FMEA)
- Systematic approach to identify potential failure modes and their effects.
Risk Priority Number (RPN)
Where:
: Severity of the effect.
: Occurrence likelihood.
: Detectability of the failure mode.
Incorporating Cascading Factors
Each parameter can be broken down into sub-factors.
Example: Component Reliability ( )
)
Where:
: Environmental factor.
: Stress factor due to usage conditions.
Sensitivity Analysis
Assess how changes in parameters affect system reliability.
Steps
- Select Parameters: Identify key parameters (
).
- Perturb Parameters: Vary each parameter within a plausible range.
- Analyze Outcomes: Observe changes in system reliability
.
- Compute Sensitivity Indices:
Bayesian Reliability Analysis
Incorporates prior knowledge and data.
Posterior Distribution
Where:
: Model parameters (e.g., failure rates).
: Prior distribution.
: Likelihood function.
Conclusion
Risk Assessment and Reliability Engineering utilize mathematical models to evaluate the reliability of systems and assess risks. By breaking down complex systems into components and modeling their interactions using tools like Fault Tree Analysis, Event Trees, and Reliability Block Diagrams, engineers can calculate system reliabilities and failure probabilities. Incorporating uncertainties, dependencies, and cascading factors is crucial for accurate assessments.
—— 4 ——
Introduction to Conservation Biology and Ecology
Conservation biology and ecology involve the study of species populations, their interactions with the environment, and the factors that influence their survival and extinction. Mathematical models are essential tools for understanding these dynamics and for making informed conservation decisions.
Key concepts include:
- Population Growth Models
- Metapopulation Dynamics
- Population Viability Analysis (PVA)
- Extinction Risk Models
- Genetic Diversity and Inbreeding
Population Growth Models
Exponential Growth Model
In an ideal environment with unlimited resources, a population grows exponentially.
Differential Equation:
Where:
: Population size
: Intrinsic rate of increase
Solution:
: Initial population size
Logistic Growth Model
In reality, resources are limited, leading to logistic growth.
Differential Equation:
Where:
: Carrying capacity of the environment
Solution:
Stochastic Population Models
Deterministic models may not capture the variability in population dynamics. Stochastic models incorporate randomness.
Stochastic Exponential Growth
Where:
: Standard deviation of the growth rate
: Increment of a Wiener process (Brownian motion)
Mean and Variance:
- Mean population size:
Variance:
Metapopulation Dynamics
Metapopulations consist of multiple subpopulations in separate habitat patches connected by dispersal.
Levins’ Metapopulation Model
Differential Equation:
Where:
: Proportion of occupied patches
: Colonization rate
: Extinction rate
Equilibrium Proportion:
Condition for Metapopulation Persistence:
Population Viability Analysis (PVA)
PVA is a quantitative method used to predict the probability of a population’s extinction over a specific time frame.
Deterministic PVA
Uses matrix models to project population growth.
Leslie Matrix Model
Used for age-structured populations.
Population Vector:
Where:
: Number of individuals in age class
at time
: Number of age classes
Leslie Matrix ():
Where:
: Fecundity of age class
: Survival rate from age class
to
Projection Equation:
Long-Term Growth Rate ():
- Dominant eigenvalue of
Stochastic PVA
Accounts for environmental and demographic stochasticity.
Stochastic Leslie Matrix
- Elements of
are random variables with specified distributions.
Simulation Steps:
- Initialize Population Vector:
- For Each Time Step:
- Sample fecundities
and survival rates
from their distributions.
- Construct
.
- Compute
.
- Sample fecundities
- Repeat for Desired Time Horizon.
Extinction Probability ():
- Estimated as the proportion of simulations where
before the end of the time horizon.
Extinction Risk Models
Deterministic Models
Quasi-Extinction Threshold ():
- Population size below which extinction is considered inevitable.
Time to Quasi-Extinction ():
Stochastic Models
Probability of Extinction in Stochastic Exponential Growth:
Genetic Diversity and Inbreeding
Loss of genetic diversity can increase extinction risk due to inbreeding depression.
Effective Population Size ( )
)
Where:
: Number of breeding males
: Number of breeding females
Inbreeding Coefficient ( )
)
Change in per generation:
Accumulated inbreeding over generations:
Incorporating Environmental Variability
Environmental stochasticity affects birth and death rates.
Modeling Environmental Variability
Let birth rate and death rate
be random variables.
Mean and Variance:
,
,
Population Growth Rate:
Variance in Growth Rate:
Incorporating Catastrophes
Rare events can have significant impacts on population dynamics.
Catastrophe Modeling
Let be the probability of a catastrophe in a time unit.
When a catastrophe occurs, the population is reduced by a fraction (survival fraction).
Effective Growth Rate:
Sensitivity and Elasticity Analysis
Assess how changes in parameters affect population growth.
Sensitivity ( )
)
Where:
: Element in the Leslie matrix
: Dominant eigenvalue (population growth rate)
Elasticity ( )
)
- Measures the proportional change in
relative to a proportional change in
.
Harvesting and Conservation Strategies
Sustainable Harvesting
Set harvest rate to maintain population at equilibrium.
Harvest Model:
Maximum Sustainable Yield (MSY):
Occurs at
MSY Harvest Rate:
Allee Effects
At low population densities, growth rates can decrease.
Allee Threshold ( )
)
Modified Logistic Equation:
- If
, the population declines.
Incorporating Habitat Loss and Fragmentation
Habitat loss reduces carrying capacity and increases extinction risk.
Time-Dependent Carrying Capacity
Where:
: Initial carrying capacity
: Habitat loss rate
Population Dynamics:
Population Extinction Time Estimation
Mean Time to Extinction ( ) for Birth-Death Processes
) for Birth-Death Processes
For small populations with :
Where:
: Birth rate per individual
: Death rate per individual
Conclusion
Mathematical models in conservation biology and ecology are vital for understanding population dynamics and assessing extinction risks. By incorporating factors such as demographic rates, environmental variability, genetic diversity, and habitat changes, these models provide insights into the viability of species and inform conservation strategies.
—— 5 ——
Climate Science: Mathematical Formulation of Carbon Footprint Calculations and Global Warming Potential
Introduction
Climate science involves understanding and modeling the Earth’s climate system and the factors that influence it. Two critical areas that use cascading factors similar to the Drake Equation are:
- Carbon Footprint Calculations: Estimating greenhouse gas emissions from various activities.
- Global Warming Potential (GWP): Assessing the relative impact of different greenhouse gases.
In this formulation, we delve into the mathematical models underlying these areas, detailing how various factors contribute to overall estimates.
Carbon Footprint Calculations
The carbon footprint measures the total greenhouse gas (GHG) emissions caused directly or indirectly by an individual, organization, event, or product. It is typically expressed in terms of carbon dioxide equivalent latex[/latex].
General Formula
The carbon footprint latex[/latex] is calculated by summing the products of activity data latex[/latex] and their corresponding emission factors latex[/latex] across all activities:
Where:
: Total carbon footprint
: Activity data for activity
(e.g., energy consumed, distance traveled)
: Emission factor for activity
Activity Data latex[/latex]
Activity data quantifies the extent of an activity that results in emissions.
Examples:
Energy Consumption:
Transportation:
Material Usage:
Emission Factors latex[/latex]
Emission factors represent the amount of GHG emissions per unit of activity.
Examples:
Electricity Emission Factor:
Fuel Combustion:
Detailed Calculation Example
Suppose we have the following activities:
Electricity Consumption:
: Electricity consumed latex[/latex]
: Emission factor
Fuel Consumption:
: Fuel consumed latex[/latex]
: Emission factor
Air Travel:
: Distance flown latex[/latex]
: Emission factor
Total Carbon Footprint:
Emission Factors Decomposition
Emission factors can be further decomposed into sub-factors.
For electricity:
Where:
: Emission factor of energy source
(e.g., coal, gas)
: Fraction of electricity from source
For fuel combustion:
Where:
: Net calorific value of the fuel latex[/latex]
: CO₂ emission factor per unit energy
: Oxidation factor (fraction of carbon not oxidized)
Global Warming Potential (GWP)
The Global Warming Potential compares the impact of different GHGs on global warming over a specified time horizon relative to CO₂.
Definition
Where:
: GWP of gas
over time horizon
: Radiative efficiency of gas
: Time-dependent concentration of gas
: Radiative efficiency of CO₂
: Time-dependent concentration of CO₂
Simplified Calculation
For practical purposes, GWP values are provided by the IPCC for standard time horizons (e.g., 20, 100 years).
Total Emissions in CO₂ Equivalent
Where:
: Mass of gas
emitted latex[/latex]
: GWP of gas
Example
- Methane (CH₄) emissions:
Nitrous oxide (N₂O) emissions:
GWP values:
,
Total CO₂ Equivalent Emissions:
Radiative Forcing and Climate Modeling
Radiative Forcing 
Radiative forcing is the change in energy flux caused by GHG concentration changes.
Where:
: Radiative forcing latex[/latex]
: Radiative efficiency of gas
: Change in concentration of gas
Temperature Change Estimation
Where:
: Change in global mean surface temperature
: Climate sensitivity parameter
Climate Feedbacks and Sensitivity
Climate Sensitivity
Climate sensitivity is the temperature change due to a doubling of CO₂ concentrations.
Where:
: Final CO₂ concentration
: Initial CO₂ concentration
For doubling CO₂ ():
Feedback Factors
Total climate feedback factor:
Where:
: Base climate sensitivity without feedbacks
: Sum of feedback factors (e.g., water vapor, ice-albedo)
Integrated Assessment Models (IAMs)
IAMs combine climate and economic models to assess policy impacts.
Emissions Pathways
Where:
: Net emissions at time
: Emissions without mitigation
: Effort for mitigation option
: Emission reduction potential of option
Discounted Cost-Benefit Analysis
Where:
: Net present value
: Benefits at time
: Costs at time
: Discount rate
: Time horizon
Uncertainty and Sensitivity Analysis
Monte Carlo Simulations
To account for uncertainties:
- Assign Distributions: For parameters like
,
.
- Sample Parameters: Generate random samples.
- Run Simulations: Compute outputs like
,
.
- Aggregate Results: Obtain distributions of outputs.
Sensitivity Analysis
Where:
: Sensitivity of output
to parameter
: Output variable (e.g.,
)
Conclusion
Climate science uses complex mathematical models to estimate greenhouse gas emissions and their impact on global warming. By cascading factors such as activity data, emission factors, radiative efficiencies, and climate sensitivities, we quantify the contributions of different activities and gases to climate change. These models are essential for informing policy decisions and mitigating the effects of global warming.
—— 6 ——
Supply Chain and Project Management: Mathematical Formulation of PERT and Supply Chain Risk Models
Introduction
Supply chain and project management involve the planning, coordination, and control of activities to achieve specific objectives efficiently. Mathematical models are essential for optimizing these processes, predicting project timelines, and assessing risks. Two critical methodologies in this field are:
- Program Evaluation and Review Technique (PERT): A statistical tool used to model project schedules under uncertainty.
- Supply Chain Risk Models: Mathematical frameworks to evaluate and mitigate risks within the supply chain.
Program Evaluation and Review Technique (PERT)
PERT is designed to analyze and represent the tasks involved in completing a project, especially when time estimates are uncertain. It uses three time estimates for each activity:
- Optimistic time (
): The shortest time in which the activity can be completed.
- Most likely time (
): The best estimate of the time required.
- Pessimistic time (
): The longest time the activity might take.
Expected Activity Duration
The expected duration () of an activity is calculated using a weighted average:
Activity Variance
The variance () of an activity’s duration reflects the uncertainty:
Critical Path Method (CPM)
The critical path is the longest path through the project network, determining the minimum project duration.
- Earliest Start Time (
) and Earliest Finish Time (
):
Latest Finish Time () and Latest Start Time (
):
Slack Time
Slack () indicates the flexibility in scheduling an activity:
Activities with zero slack are critical and cannot be delayed without affecting the project completion time.
Project Completion Time
The expected project completion time () is determined by summing the expected durations along the critical path.
Project Variance
The project variance () is the sum of variances of activities on the critical path:
Probability of Completing by a Target Date
Assuming a normal distribution of project completion times:
: Target completion time.
: Standard normal variable.
- The probability (
) of completing the project by time
:
Where is the cumulative distribution function of the standard normal distribution.
Supply Chain Risk Models
Supply chain risk models evaluate the probability and impact of disruptions in the supply chain by analyzing various risk factors.
Overall Supply Chain Reliability
The overall reliability () of a supply chain is the product of the reliabilities of its components:
: Reliability of component
(e.g., supplier, transport link).
Probability of Supply Chain Failure
The probability of failure () is:
Modeling Component Reliability
Each component’s reliability can be affected by multiple factors.
Supplier Reliability
can be broken down:
Where:
: Reliability regarding product quality.
: On-time delivery reliability.
: Financial stability of the supplier.
Transportation Reliability
accounts for risks like delays (
) and accidents (
):
Demand Variability and Forecasting
Demand variability impacts inventory levels and stockout risks.
- Standard Deviation of Demand (
).
- Lead Time Demand (
):
: Mean demand per period.
: Lead time in periods.
Safety Stock Calculation
To achieve a desired service level ():
: Z-score corresponding to
.
Inventory Risk of Stockout
The probability of stockout () during lead time:
Risk Mitigation Strategies
Redundancy
Implementing backup suppliers or alternative routes:
- Parallel Reliability:
Diversification
Sourcing from multiple suppliers to reduce dependency.
Contingency Planning
Preparing response strategies for potential disruptions.
Event Tree Analysis (ETA)
ETA models the possible outcomes following an initiating event.
Calculating Scenario Probabilities
For a sequence of events:
: Probability of event
.
Expected Loss
: Consequence (cost) of scenario
.
Bayesian Networks in Supply Chain Risk
Bayesian networks capture dependencies among risk factors.
Joint Probability Distribution
: A random variable representing a risk factor.
Sensitivity Analysis
Evaluating how changes in parameters affect overall risk.
Sensitivity Coefficient
: Parameter (e.g.,
).
Monte Carlo Simulation
To handle uncertainty in parameters:
- Define Probability Distributions: For uncertain parameters.
- Random Sampling: Generate random values for parameters.
- Model Evaluation: Compute
for each sample.
- Statistical Analysis: Assess risk levels and confidence intervals.
Conclusion
Mathematical modeling in supply chain and project management enables better planning, risk assessment, and decision-making. PERT provides a structured approach to estimate project durations under uncertainty, while supply chain risk models help identify vulnerabilities and optimize strategies to enhance reliability and resilience.
—— 7 ——
Security and Defense Analysis: Mathematical Formulation of Kill Chain Models and Terrorism Risk Assessment
Introduction
Security and defense analysis involves evaluating the effectiveness of defensive measures and assessing the risks associated with potential threats. Mathematical models play a crucial role in quantifying these aspects, enabling decision-makers to allocate resources effectively and enhance security measures. Two primary methodologies in this domain that utilize cascading factors are:
- Kill Chain Models
- Terrorism Risk Assessment
Kill Chain Models
The kill chain is a military concept that defines the structure of an attack by breaking it down into a series of stages. Each stage must be successfully completed for the attack to be effective. The stages typically include:
- Detection
- Identification
- Tracking
- Engagement
- Assessment
Overall Mission Success Probability
The overall probability of mission success () is the product of the probabilities of success at each stage:
Where:
: Probability of success at stage
: Total number of stages in the kill chain
Stage-wise Probability Modeling
Each stage’s probability can be modeled based on specific factors.
Detection Probability ( )
)
Where:
: Cross-section or detectability factor of the target
: Distance to the target
: Environmental or sensor-specific exponent
Identification Probability ( )
)
Where:
: Time available for identification
- Function
accounts for factors like operator proficiency and system capabilities
Engagement Probability ( )
)
: Probability of successful weapon launch
: Probability that the weapon intercepts the target
: Probability that the weapon destroys the target upon interception
Cumulative Probability Distribution
The cumulative distribution function (CDF) of mission success is:
Where:
: Effective rate of mission success
: Time
Terrorism Risk Assessment
Terrorism risk assessment evaluates the likelihood and potential impact of terrorist activities to inform security measures and resource allocation.
Overall Risk Calculation
Risk () is typically calculated as:
Where:
: Threat likelihood
: Vulnerability of the target
: Consequence or impact of an attack
Threat Likelihood ( )
)
Threat likelihood is a function of:
Where:
: Intent of the adversary
: Capability of the adversary to carry out the attack
Modeling Intent ( )
)
: Motivating factors (e.g., ideological, political)
: Deterrence measures in place
Modeling Capability ( )
)
: Available resources (e.g., funding, equipment)
: Skill level of adversaries
: Access to the target or necessary information
Vulnerability (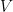 )
)
Vulnerability represents the probability that an attack on a target would be successful.
Where:
: Effectiveness of defensive measures
Modeling Defensive Effectiveness
: Probability that defenses deter an attack
: Probability of detecting an attack before it occurs
: Probability of effectively responding to an attack
Consequence (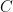 )
)
Consequences are quantified based on potential losses, including:
: Loss of life and injuries
: Financial costs due to damage and disruption
: Societal impact and loss of public confidence
Risk Assessment Models
Event Tree Analysis (ETA)
ETA models possible attack scenarios and their probabilities.
- Initiating Event: Occurrence of an attack attempt.
- Branches: Success or failure at each stage due to defensive measures.
Probability of a Scenario
Where:
: Probability of attack attempt
: Probability of success or failure at stage
Bayesian Networks
Bayesian networks capture dependencies among variables in risk assessment.
- Nodes: Represent variables (e.g., threat level, vulnerability).
- Edges: Represent dependencies.
Joint Probability Distribution
Resource Allocation Models
Optimizing resource allocation to minimize risk.
Objective Function
Subject to:
Where:
: Allocation of resources to different security measures
: Total budget available
: Vulnerability as a function of resource allocation
Constraints
- Budget Constraint:
: Cost of implementing measure
Effectiveness Constraint:
Game Theoretic Models
Analyzing interactions between defenders and adversaries.
Payoff Matrix
Defender’s strategies () and attacker’s strategies (
):
- Defender’s Payoff:
Attacker’s Payoff:
Where:
: Cost of defense measures
: Cost to the attacker
: Value or benefit to the attacker upon success
Nash Equilibrium
A strategy profile where neither player can unilaterally improve their payoff.
Sensitivity Analysis
Assessing how changes in parameters affect overall risk.
Sensitivity Coefficient
Where:
: Parameter (e.g.,
,
,
)
: Overall risk
Uncertainty and Monte Carlo Simulation
Accounting for uncertainties in parameters.
Steps:
- Define Probability Distributions: For uncertain parameters (e.g., threat likelihood, vulnerability).
- Random Sampling: Generate random samples using these distributions.
- Model Evaluation: Compute risk (
) for each sample.
- Statistical Analysis: Determine confidence intervals and probability distributions of risk.
Conclusion
Mathematical models in security and defense analysis are vital for quantifying risks and optimizing defense strategies. By modeling cascading factors such as threat likelihood, vulnerability, and consequences, these models help in making informed decisions to enhance security measures and allocate resources effectively.
—— 8 ——
Public Health Policy: Mathematical Formulation of Health Impact Assessments and Multi-Criteria Decision Analysis
Introduction
Public health policy involves the development and implementation of strategies to improve population health outcomes. Mathematical models play a crucial role in evaluating the potential impacts of policies, prioritizing interventions, and informing decision-making. Two key methodologies in this domain that utilize cascading factors are:
- Health Impact Assessments (HIA)
- Multi-Criteria Decision Analysis (MCDA)
Health Impact Assessments (HIA)
HIA is a systematic process that evaluates the potential health effects of a policy, program, or project on a population. It incorporates quantitative and qualitative methods to predict health outcomes based on exposure levels, dose-response relationships, and population characteristics.
General Framework of HIA
The overall health impact () can be estimated using the following equation:
Where:
: Exposure level to risk factor
: Dose-response function for health outcome associated with risk factor
: Population exposed to risk factor
: Number of risk factors considered
Exposure Assessment
Exposure level () is determined based on environmental concentrations and individual behaviors.
Where:
: Concentration of pollutant or risk factor
- Intake Rate: Rate at which individuals come into contact with
- Exposure Duration: Time period over which exposure occurs
Dose-Response Relationship
The dose-response function () quantifies the relationship between exposure and health outcome.
Linear Model:
Where is the slope of the dose-response curve for risk factor
.
Non-Linear Model:
Where and
are parameters estimated from epidemiological studies.
Population Attributable Fraction (PAF)
The PAF represents the proportion of incidents that can be attributed to a specific risk factor.
Where:
: Prevalence of exposure to risk factor
: Relative risk associated with exposure to
Estimating Health Outcomes
The number of cases prevented or caused () due to changes in exposure is:
Where:
: Baseline number of cases in the population
Disability-Adjusted Life Years (DALYs)
DALYs measure the overall disease burden.
Where:
: Disability weight for health outcome
: Average duration of the health outcome
Multi-Criteria Decision Analysis (MCDA)
MCDA is a decision-making framework that evaluates and prioritizes options based on multiple criteria. It involves assigning weights to criteria and scoring options against these criteria.
General Framework of MCDA
The overall score () for option
is calculated as:
Where:
: Weight of criterion
: Score of option
on criterion
: Number of criteria
Weighting Criteria
Weights reflect the relative importance of each criterion.
- Normalization:
Methods to Determine Weights:
- Expert Judgment
- Analytic Hierarchy Process (AHP)
- Swing Weighting
Scoring Options
Scores represent how well each option performs on each criterion.
- Scaling:Scores are normalized to a common scale, e.g., 0 to 1.
- Performance Matrix:
Where:
: Number of options
Ranking and Selection
Options are ranked based on their overall scores (). The option with the highest score is considered the most favorable.
Combining HIA and MCDA
In public health policy, HIA can provide quantitative estimates of health impacts, which can be integrated into MCDA as criteria.
Example Integration
- Criteria:
- Health Impact (
): Measured in DALYs prevented
- Cost (
): Financial cost of implementation
- Equity (
): Distribution of benefits across populations
- Feasibility (
): Practicality of implementation
- Health Impact (
- Weights:
determined based on stakeholder preferences
- Scores:
- Calculated for each policy option using normalized scales
Uncertainty Analysis
Both HIA and MCDA involve uncertainties due to data limitations and variability.
Monte Carlo Simulation
To quantify uncertainties, Monte Carlo simulations can be used.
- Define Probability Distributions for uncertain parameters (e.g., exposure levels, dose-response coefficients, weights).
- Random Sampling: Generate random samples from these distributions.
- Model Evaluation: Compute
and
for each simulation.
- Statistical Analysis: Obtain confidence intervals and probability distributions for outputs.
Sensitivity Analysis
Assess the influence of individual parameters on the outcomes.
- One-Way Sensitivity Analysis: Vary one parameter at a time.
- Tornado Diagrams: Visualize the impact of parameters on results.
Ethical and Equity Considerations
Mathematical models should account for ethical considerations and health equity.
Equity Weighting
Adjust weights or scores to reflect the importance of health impacts on vulnerable populations.
Where:
: Equity factor for criterion
Policy Optimization
Use mathematical programming to identify the optimal mix of interventions.
Objective Function
Subject to:
(Binary decision variables)
: Total budget
Conclusion
Mathematical formulations in public health policy, such as HIA and MCDA, provide a structured approach to evaluate the potential health impacts of policies and to make informed decisions by considering multiple criteria. By incorporating cascading factors like exposure levels, dose-response relationships, and stakeholder preferences, these models help policymakers optimize interventions to improve public health outcomes.
—— 9 ——
Environmental Impact Studies: Mathematical Formulation of Life Cycle Assessment and Cumulative Risk Assessment
Introduction
Environmental impact studies aim to evaluate the potential environmental consequences of projects, policies, or products. Mathematical models are essential tools in quantifying these impacts, enabling informed decision-making and mitigation strategies. Two key methodologies that involve cascading factors similar to the Drake Equation are:
- Life Cycle Assessment (LCA)
- Cumulative Risk Assessment (CRA)
Life Cycle Assessment (LCA)
LCA is a systematic method for evaluating the environmental aspects associated with a product, process, or service throughout its life cycle, from raw material extraction through production, use, and disposal.
Phases of LCA
- Goal and Scope Definition
- Inventory Analysis
- Impact Assessment
- Interpretation
Life Cycle Inventory (LCI)
The LCI quantifies energy and raw material inputs and environmental releases throughout the life cycle.
Data Collection
For each process or activity, collect data on:
- Inputs: Raw materials, energy, water
- Outputs: Emissions to air, water, and soil; solid waste; products
Mathematical Formulation
The total environmental impact () is calculated by summing the impacts of all life cycle stages:
Where:
: Activity level or amount of process
: Environmental impact per unit of process
: Number of processes in the life cycle
Activity Level ( )
)
The activity level represents the quantity of a process or activity.
Where:
: Flow coefficient representing the amount of process
required per unit of product
: Production volume of product
: Number of products
Environmental Impact per Unit Process ( )
)
Where:
: Quantity of emission or resource
per unit of process
: Characterization factor for emission or resource
: Number of emissions and resources considered
Impact Assessment
In the impact assessment phase, the environmental impacts are categorized and quantified.
Classification
Assign each emission or resource use to impact categories (e.g., global warming, acidification).
Characterization
Calculate category indicator results using characterization factors.
Where:
: Emission or resource use
: Characterization factor for
in the category
Normalization (Optional)
Weighting (Optional)
Assign weights to impact categories based on their relative importance.
Where:
: Weight assigned to the impact category
Life Cycle Impact Assessment (LCIA) Modeling
Using matrices to represent the system:
- Technology Matrix (
):Represents the inputs and outputs between processes.
- Intervention Matrix (
):Represents environmental interventions (emissions, resource extractions).
- Characterization Matrix (
):Contains characterization factors.
Calculations
Solve for Activity Levels:
Where:
: Vector of process activity levels
: Demand vector for final products
Solve for :
Calculate Environmental Interventions:
Where : Vector of total emissions and resource uses
Calculate Impact Categories:
Where : Vector of category indicator results
Cumulative Risk Assessment (CRA)
CRA evaluates the combined risks from multiple environmental stressors affecting human health or ecosystems.
General Framework
- Problem Formulation
- Exposure Assessment
- Dose-Response Assessment
- Risk Characterization
Exposure Assessment
Determine the cumulative exposure from all sources and pathways.
Where:
: Concentration of stressor
: Intake rate for stressor
: Exposure frequency for stressor
: Exposure duration for stressor
: Number of stressors
Dose-Response Assessment
Assess the relationship between dose and adverse effects.
- Non-Cancer Effects:
Where:
: Hazard quotient for stressor
: Exposure dose for stressor
: Reference dose for stressor
Cancer Effects:
Where:
: Cancer risk from stressor
: Slope factor for stressor
Risk Characterization
Aggregate risks across stressors and pathways.
Non-Cancer Hazard Index (HI):
Cancer Risk:
Considering Interactions
Adjust for interactions among stressors.
- Additive Effects:Assume risks are additive unless evidence suggests otherwise.
- Synergistic or Antagonistic Effects:
Where:
: Interaction factor for stressor
Uncertainty Analysis
Address uncertainties in data and models.
- Monte Carlo Simulation:
- Define probability distributions for uncertain parameters.
- Run simulations to generate a range of possible outcomes.
- Analyze the results to estimate confidence intervals.
- Sensitivity Analysis:Identify parameters that significantly influence the results.
Combining LCA and CRA
For comprehensive environmental impact studies, integrate LCA and CRA to assess both ecological and human health impacts.
Integrated Impact Assessment
- Calculate Life Cycle Emissions using LCA methods.
- Assess Human Health Risks from emissions using CRA methods.
Where:
: Exposure from life cycle emissions of pollutant
: Slope factor or potency of pollutant
Conclusion
Mathematical models in environmental impact studies, such as LCA and CRA, provide a structured approach to quantify the potential environmental and health impacts associated with products, processes, or policies. By cascading factors like activity levels, emissions, exposures, and dose-response relationships, these models help decision-makers identify significant contributors to impacts and develop strategies for mitigation.
—— 10 ——
Financial Risk Modeling and Portfolio Optimization: Mathematical Formulation of Market Dynamics and Risk Analysis
Introduction
Financial risk modeling and portfolio optimization involve mathematical techniques to assess market risks, optimize investment portfolios, and make informed financial decisions. These models incorporate various factors such as asset returns, risk measures, and constraints to maximize returns while minimizing risks.
Modern Portfolio Theory (MPT)
MPT, introduced by Harry Markowitz, aims to construct portfolios that optimize expected return for a given level of risk.
Expected Return
The expected return () of a portfolio is:
Where:
: Weight of asset
in the portfolio
: Expected return of asset
: Number of assets
Portfolio Variance
The portfolio variance () is:
Where:
: Covariance between assets
and
Covariance Matrix
Optimization Problem
Minimize portfolio variance subject to expected return:
Where:
: Weight vector
: Expected return vector
Capital Asset Pricing Model (CAPM)
CAPM describes the relationship between systematic risk and expected return.
Security Market Line (SML)
Where:
: Expected return of asset
: Risk-free rate
: Beta of asset
: Expected return of the market portfolio
Beta Calculation
Where:
: Covariance between asset
and the market
: Variance of market returns
Value at Risk (VaR)
VaR quantifies the potential loss in value of a portfolio over a defined period for a given confidence interval.
VaR Formula
Where:
: Expected portfolio return
: Portfolio standard deviation
: Z-score corresponding to confidence level
Risk Measures
Expected Shortfall (ES)
ES measures the expected loss in the worst fraction of cases.
Portfolio Optimization with Constraints
Incorporate constraints such as transaction costs, taxes, and regulatory requirements.
Optimization Problem with Constraints
Where:
: Minimum desired return
,
: Matrices representing additional constraints
Black-Scholes Option Pricing Model
Calculates the theoretical price of European call and put options.
Black-Scholes Formula for Call Option
Where:
: Current stock price
: Strike price
: Risk-free interest rate
: Time to maturity
: Cumulative distribution function of the standard normal distribution
: Volatility of the stock
Arbitrage Pricing Theory (APT)
An asset’s returns can be modeled as a linear function of various macroeconomic factors.
Factor Model
Where:
: Return on asset
: Asset-specific constant
: Sensitivity of asset
to factor
: Factor
: Idiosyncratic error term
Risk-Neutral Valuation
Used for pricing derivatives by constructing a risk-neutral probability measure.
Martingale Pricing
Where:
: Value of the derivative at time
: Payoff at maturity
: Risk-neutral probability measure
: Information available at time
Credit Risk Modeling
Assessing the risk of loss due to a borrower’s failure to make payments.
Probability of Default (PD)
Modeled using logistic regression or structural models.
Loss Given Default (LGD)
The proportion of the exposure that is lost if a default occurs.
Expected Loss (EL)
Where:
: Exposure at default
Monte Carlo Simulation
Used for estimating the distribution of portfolio returns and risks.
Steps
- Generate Random Asset Returns using assumed distributions.
- Calculate Portfolio Returns for each simulation.
- Aggregate Results to estimate risk measures like VaR and ES.
Conclusion
Mathematical models in financial risk modeling and portfolio optimization are essential for managing investments, assessing risks, and making informed financial decisions. By incorporating factors such as expected returns, variances, covariances, and constraints, these models help optimize portfolios to achieve desired risk-return profiles.
Write an essay on the commonalities among these ten complex systems and the cross-domain insights.
Title: Commonalities Among Diverse Complex Systems and Cross-Domain Insights
Introduction
The ten systems explored—ranging from astrobiology to financial risk modeling—may appear disparate at first glance. However, they share remarkable commonalities in their mathematical formulations and the methodologies used to understand their dynamics. Each system deals with complex interactions, uncertainties, and the need to make informed decisions based on quantitative analysis. This essay delves into the shared characteristics among these systems and highlights the cross-domain insights that emerge from their study.
Common Mathematical Frameworks
1. Cascading Factors and Multiplicative Models
A unifying feature among these systems is the use of cascading factors in multiplicative models to estimate outcomes:
- Astrobiology and Exoplanet Studies: The Seager Equation multiplies factors like the number of stars observed, fraction of quiet stars, and probabilities of habitable conditions to estimate the number of detectable biosignatures.
- Epidemiology: The basic reproduction number (
) is a product of factors such as transmission rate, contact rate, and duration of infectiousness.
- Risk Assessment: Fault Tree Analysis calculates the probability of a top event (system failure) by multiplying the probabilities of basic events (component failures).
- Climate Science: Carbon footprint calculations multiply activity data by emission factors to estimate total emissions.
These multiplicative models reflect how complex outcomes depend on a series of interrelated factors, emphasizing the importance of understanding each component’s contribution.
2. Probabilistic and Statistical Methods
All systems incorporate probabilistic approaches to account for uncertainties:
- Monte Carlo Simulations: Used extensively across domains (e.g., epidemiology, financial risk modeling, supply chain risk analysis) to model uncertainties by sampling from probability distributions.
- Bayesian Frameworks: Employed in advanced statistical modeling (e.g., astrobiology, risk assessment) to update probabilities as new data become available.
- Stochastic Modeling: Applied in epidemiology (e.g., stochastic SIR models), conservation biology (e.g., population viability analysis), and financial markets (e.g., stock price movements).
These methods enable practitioners to quantify uncertainties and make probabilistic predictions about system behaviors.
3. Sensitivity and Uncertainty Analysis
Assessing the impact of parameter changes is crucial:
- Sensitivity Analysis: Identifies which parameters most significantly affect outcomes, guiding resource allocation and policy decisions. For instance, in public health policy, sensitivity analysis can determine which interventions most effectively reduce disease spread.
- Uncertainty Quantification: Provides confidence intervals and risk assessments, essential in fields like climate science and financial risk modeling.
4. Hierarchical and Network Models
Many systems use hierarchical structures or networks to represent interactions:
- Epidemiology and Ecology: Use compartmental models and food webs to represent interactions between species or disease states.
- Supply Chain Management: Models the supply chain as a network of suppliers, manufacturers, and distributors.
- Security and Defense: Employ kill chain models and network analysis to understand potential attack pathways.
These models capture the complexity of systems where components interact at multiple levels.
5. Optimization Techniques
Optimization is fundamental in decision-making processes:
- Portfolio Optimization: In financial modeling, optimization algorithms maximize returns while minimizing risks under certain constraints.
- Resource Allocation: In public health and security, mathematical programming optimizes the allocation of limited resources to maximize impact or minimize risk.
6. Use of Differential Equations
Differential equations model the dynamic changes in systems:
- Epidemiology: SIR and SEIR models use differential equations to describe disease spread.
- Conservation Biology: Population growth models use differential equations to predict changes over time.
- Climate Models: Employ differential equations to simulate atmospheric and oceanic processes.
Cross-Domain Insights
1. Interdisciplinary Methodologies Enhance Understanding
The mathematical tools developed in one domain can be adapted to others:
- Network Theory: Used in epidemiology to model disease transmission and in supply chain management to optimize logistics.
- Risk Assessment Techniques: Fault tree analysis in engineering can inform risk models in finance and security.
This cross-pollination of methodologies fosters innovation and more robust models.
2. Managing Uncertainty is Universal
All systems face uncertainties due to incomplete data, variability, or inherent randomness:
- Climate Science: Uncertainties in emission factors and climate sensitivity necessitate probabilistic models.
- Financial Markets: Volatility and unforeseen events require risk models that can handle stochastic processes.
- Public Health: Variability in human behavior and pathogen characteristics demands flexible models.
Understanding and quantifying uncertainties allow for better risk management and decision-making.
3. Importance of Sensitivity Analysis Across Domains
Identifying critical factors is essential for effective intervention:
- Conservation Biology: Sensitivity analysis can reveal which species or habitats are most crucial to protect.
- Supply Chain Management: Determines which suppliers or transport links are critical points of failure.
- Security and Defense: Highlights vulnerabilities in systems that require strengthening.
Focusing on key factors maximizes the efficiency of interventions.
4. Ethical and Societal Implications
Mathematical models have significant impacts on society:
- Public Health Policy: Decisions based on models affect resource distribution and can have ethical considerations regarding equity and justice.
- Environmental Impact Studies: Assessments influence regulations that balance economic development with environmental protection.
- Security Measures: Models inform policies that must consider civil liberties and privacy concerns.
Integrating ethical considerations into modeling ensures that outcomes align with societal values.
5. Necessity of Multi-Scale Modeling
Systems operate at multiple scales, requiring models that can integrate different levels:
- Climate Science: Models range from global climate patterns to local weather events.
- Epidemiology: Must consider individual behaviors up to population-level trends.
- Financial Markets: Micro-level trading impacts macroeconomic indicators.
Multi-scale models provide a comprehensive understanding of system dynamics.
6. Data-Driven Decision Making
Empirical data inform model parameters and validate predictions:
- Health Impact Assessments: Use epidemiological data to estimate dose-response relationships.
- Financial Models: Rely on historical market data to forecast future trends.
- Environmental Assessments: Utilize emissions data and environmental measurements.
Data-driven models enhance accuracy and reliability.
Conclusion
The exploration of these ten diverse systems reveals that complex, real-world problems often require similar mathematical approaches. Commonalities such as the use of cascading factors, probabilistic methods, sensitivity analysis, and optimization techniques underscore the interconnectedness of different fields. Cross-domain insights demonstrate that methodologies developed in one area can significantly enhance understanding and problem-solving in another. Embracing these commonalities fosters interdisciplinary collaboration, leading to more robust models and better-informed decisions that can address the multifaceted challenges of our world.
Quiz
#1: What does the Seager Equation in astrobiology estimate?
Answer:
The Seager Equation estimates the number of planets with detectable signs of life. It factors in the number of observed stars, the fraction of stars with habitable planets, and other conditions that make life and biosignatures detectable.#2: In epidemiology, what are the three main compartments in the SIR model?
Answer:
The three main compartments are: – Susceptible (S): Individuals who can contract the disease. – Infectious (I): Individuals who have the disease and can spread it. – Recovered (R): Individuals who have recovered and gained immunity.#3: What is Fault Tree Analysis (FTA), and how is it used in risk assessment?
Answer:
Fault Tree Analysis (FTA) is a top-down approach to identify the root causes of system failures. It uses logic gates (AND, OR) to calculate the probability of the system failing based on the failure probabilities of individual components.#4: What is Population Viability Analysis (PVA) used for in conservation biology?
Answer:
Population Viability Analysis (PVA) is used to predict the probability of a population’s extinction over a specific time period. It helps assess the long-term viability of species and inform conservation strategies.#5: What two main components are involved in calculating a carbon footprint?
Answer:
A carbon footprint is calculated by multiplying: 1. Activity data (e.g., energy consumption, distance traveled). 2. Emission factors (the amount of greenhouse gas emissions per unit of activity).#6: What are the three time estimates used in PERT, and how is the expected activity duration calculated?
Answer:
The three time estimates in PERT are: – Optimistic (O) – Most Likely (M) – Pessimistic (P) The expected activity duration is calculated using the formula: Expected Duration = (O + 4M + P) / 6.#7: What is a kill chain model, and how is it used in security and defense analysis?
Answer:
A kill chain model breaks down the sequence of events an adversary takes during an attack (e.g., detection, identification, engagement). It helps identify stages where defensive actions can be taken to disrupt the attack.#8: What is the purpose of a Health Impact Assessment (HIA) in public health policy?
Answer:
A Health Impact Assessment (HIA) evaluates the potential health effects of a policy, project, or program on a population. It uses data on exposure levels, dose-response relationships, and population characteristics to predict health outcomes.#9: What are the four main phases of Life Cycle Assessment (LCA)?
Answer:
The four main phases of Life Cycle Assessment (LCA) are: 1. Goal and Scope Definition. 2. Inventory Analysis. 3. Impact Assessment. 4. Interpretation.#10: What is the primary objective of Modern Portfolio Theory (MPT)?
Answer:
The primary objective of Modern Portfolio Theory (MPT) is to optimize the expected return of an investment portfolio for a given level of risk by diversifying assets and minimizing portfolio variance.#11: How do probabilistic methods help in managing uncertainty across different systems?
Answer:
Probabilistic methods, such as Monte Carlo simulations and Bayesian analysis, help manage uncertainty by modeling randomness and variability. They provide a range of potential outcomes and their probabilities, allowing for more informed decisions under uncertainty.#12: Why is sensitivity analysis important in mathematical models of complex systems?
Answer:
Sensitivity analysis is important because it identifies the parameters that most significantly impact model outcomes. This helps focus resources on key factors and improves decision-making by understanding which variables drive changes in the system.#13: How are network models used in epidemiology and supply chain management?
Answer:
– In epidemiology, network models represent how individuals interact and spread diseases within a population. – In supply chain management, network models depict the relationships between suppliers, manufacturers, and distributors, helping to optimize logistics and manage risks.#14: What is the role of optimization techniques in decision-making processes across different fields?
Answer:
Optimization techniques help identify the best possible solution to a problem by maximizing or minimizing an objective function. For example, in finance, optimization is used to maximize returns while minimizing risk; in public health, it optimizes resource allocation to maximize impact.#15: How are differential equations used in dynamic systems modeling?
Answer:
Differential equations describe the rate of change of variables over time and are used to model dynamic processes. For instance, in epidemiology, they model how diseases spread over time; in climate science, they simulate environmental processes like temperature changes.#16: How do interdisciplinary methodologies enhance the understanding of complex systems?
Answer:
Interdisciplinary methodologies allow for the application of tools and concepts from one field to another, fostering innovation and more comprehensive models. For example, network theory can enhance models of disease spread, and risk assessment techniques can improve financial modeling.#17: Why is managing uncertainty a universal challenge in modeling complex systems?
Answer:
Uncertainty arises from incomplete data, variability, and randomness. Managing uncertainty is crucial for making reliable predictions and decisions. Quantifying uncertainties helps plan for different scenarios and better manage risks across all domains.#18: What is the necessity of multi-scale modeling in understanding complex systems?
Answer:
Multi-scale modeling integrates processes occurring at different spatial or temporal scales to capture the full complexity of a system. For example, in climate science, both global patterns and local weather events need to be modeled for a comprehensive understanding.#19: How does data-driven decision-making play a role across different domains?
Answer:
Data-driven decision-making uses empirical data to inform models, validate predictions, and guide policies or investments. For example, public health decisions rely on epidemiological data, while financial models use historical market data to make investment forecasts.#20: What are some common mathematical approaches shared among the ten systems discussed?
Answer:
Common approaches include: – Cascading factors in multiplicative models. – Probabilistic and statistical methods to manage uncertainty. – Sensitivity analysis to identify critical factors. – Network and hierarchical models to represent interactions. – Optimization techniques to find optimal solutions under constraints. – Use of differential equations to model dynamic changes over time.Provide 25 discussion questions relevant to the content above.
Astrobiology and Exoplanet Studies
- How does the Seager Equation account for the various factors influencing the detectability of biosignatures on exoplanets?
- What are the limitations of the Seager Equation in estimating the number of habitable planets, and how can these limitations be addressed?
Epidemiology
- In what ways can stochastic SIR models provide more accurate predictions of disease spread compared to deterministic models?
- How can sensitivity analysis in epidemiological models inform public health interventions during an outbreak?
Risk Assessment and Reliability Engineering
- How does Fault Tree Analysis (FTA) help in identifying critical components within a complex system?
- What are the advantages and disadvantages of using Bayesian Networks in Probabilistic Risk Assessment (PRA)?
Conservation Biology and Ecology
- How can Population Viability Analysis (PVA) be integrated with genetic diversity models to enhance conservation strategies?
- What role do environmental stochasticity and demographic stochasticity play in the extinction risk of endangered species?
Climate Science
- How do cascading factors in carbon footprint calculations influence the overall assessment of greenhouse gas emissions?
- In what ways can Global Warming Potential (GWP) metrics be improved to better reflect the long-term impacts of various greenhouse gases?
Supply Chain and Project Management
- How can the Program Evaluation and Review Technique (PERT) be adapted to manage projects with highly uncertain timelines?
- What mathematical approaches can be used to optimize supply chain resilience against potential disruptions?
Security and Defense Analysis
- How can kill chain models be enhanced with probabilistic methods to better predict and prevent security breaches?
- What are the ethical considerations when using mathematical models for terrorism risk assessment?
Public Health Policy
- How can Health Impact Assessments (HIA) be integrated with Multi-Criteria Decision Analysis (MCDA) to inform comprehensive public health policies?
- What are the challenges in quantifying dose-response relationships in Health Impact Assessments?
Environmental Impact Studies
- How does Life Cycle Assessment (LCA) contribute to sustainable product development, and what are its key mathematical components?
- In Cumulative Risk Assessment (CRA), how can interactions among multiple stressors be effectively modeled?
Financial Risk Modeling and Portfolio Optimization
- How does Modern Portfolio Theory (MPT) balance the trade-off between risk and return in investment portfolios?
- What are the key differences between Value at Risk (VaR) and Expected Shortfall (ES) as risk measures in financial modeling?
Cross-Domain Methodologies
- In what ways can network theory developed in epidemiology be applied to enhance supply chain risk management?
- How can optimization techniques used in financial portfolio management be adapted for resource allocation in public health policy?
Managing Uncertainty
- Discuss the role of Monte Carlo simulations in handling uncertainty across different modeling domains.
- How can Bayesian frameworks improve the accuracy of predictions in environmental impact studies?
Sensitivity Analysis
- Why is sensitivity analysis critical in both climate science models and financial risk assessments?
- How can sensitivity indices guide decision-making in conservation biology?
Hierarchical and Network Models
- Compare the use of hierarchical models in conservation biology with network models in security and defense analysis.
- What are the benefits of using multi-level network models in epidemiology?
Optimization Techniques
- How can multi-objective optimization be utilized in balancing economic and environmental goals in public health policy?
- Discuss the application of linear programming in supply chain risk mitigation strategies.
Differential Equations in Dynamic Systems
- Explain how differential equations model the spread of infectious diseases and climate change simultaneously.
- What are the challenges of solving non-linear differential equations in financial risk modeling?
Interdisciplinary Methodologies
- Provide examples of how interdisciplinary approaches have led to breakthroughs in two different domains discussed above.
- How can lessons learned from risk assessment in engineering inform security and defense models?
Ethical and Societal Implications
- What ethical considerations arise when using predictive models in public health policy?
- How can mathematical models in environmental impact studies ensure equitable outcomes for vulnerable populations?
Multi-Scale Modeling
- Discuss the importance of integrating micro-level behaviors with macro-level trends in climate science models.
- How does multi-scale modeling enhance the accuracy of Population Viability Analysis (PVA)?
Data-Driven Decision Making
- How does the availability of high-quality data influence the effectiveness of financial risk models and public health policies?
- What are the potential biases in data-driven models, and how can they be mitigated across different domains?
Common Mathematical Approaches
- Identify and explain two mathematical approaches that are common across at least three different systems discussed.
- How do cascading factors in mathematical models highlight the interconnectedness of various system components?
Model Integration
- How can integrating Life Cycle Assessment (LCA) with Cumulative Risk Assessment (CRA) provide a more comprehensive understanding of environmental impacts?
- What are the challenges and benefits of combining epidemiological models with public health policy frameworks?
Resource Allocation
- In what ways can portfolio optimization techniques be applied to optimize resource allocation in supply chain management?
- How can optimization models balance multiple criteria in Multi-Criteria Decision Analysis (MCDA) for public health interventions?
Risk Mitigation Strategies
- Compare the effectiveness of redundancy and diversification as risk mitigation strategies in supply chain and financial portfolio management.
- How can contingency planning be mathematically modeled to improve supply chain resilience?
Future Directions and Innovations
- What emerging mathematical techniques could enhance the modeling of complex systems in the next decade?
- How can advancements in computational power and data analytics transform traditional models in the systems discussed?
Table of Contents: (Click any link below to navigate to that section.)
- List fields of exploration similar to the Drake Equation in which there are cascading interdependent factors.
- Provide a robust, comprehensive mathematical formulation of the dynamics for each field.
- —— 1 —— The Seager Equation
- —— 2 —— Introduction to Epidemiological Modeling
- Basic Reproduction Number (R₀)
- Compartmental Models
- Basic Reproduction Number in the SIR Model
- Threshold Behavior
- SEIR Model
- Chain Binomial Models
- Stochastic Modeling
- Next-Generation Matrix
- Epidemic Modeling with Age Structure
- Network Models
- Metapopulation Models
- Control Measures
- Incorporating Cascading Factors
- Parameter Estimation
- Sensitivity Analysis
- Uncertainty Quantification
- Conclusion
- —— 3 —— Introduction to Risk Assessment and Reliability Engineering
- Reliability Theory
- Series and Parallel Systems
- Fault Tree Analysis (FTA)
- Minimal Cut Sets
- Reliability Block Diagrams (RBD)
- Probabilistic Risk Assessment (PRA)
- Bayesian Networks
- Markov Models
- Importance Measures
- Uncertainty Analysis
- Reliability Growth Modeling
- Common Cause Failures
- Life Data Analysis
- System Availability
- Failure Modes and Effects Analysis (FMEA)
- Incorporating Cascading Factors
- Sensitivity Analysis
- Bayesian Reliability Analysis
- Conclusion
- —— 4 —— Introduction to Conservation Biology and Ecology
- Population Growth Models
- Stochastic Population Models
- Metapopulation Dynamics
- Population Viability Analysis (PVA)
- Extinction Risk Models
- Genetic Diversity and Inbreeding
- Incorporating Environmental Variability
- Incorporating Catastrophes
- Sensitivity and Elasticity Analysis
- Harvesting and Conservation Strategies
- Allee Effects
- Incorporating Habitat Loss and Fragmentation
- Population Extinction Time Estimation
- Conclusion
- —— 5 —— Climate Science: Mathematical Formulation of Carbon Footprint Calculations and Global Warming Potential
- —— 6 —— Supply Chain and Project Management: Mathematical Formulation of PERT and Supply Chain Risk Models
- —— 7 —— Security and Defense Analysis: Mathematical Formulation of Kill Chain Models and Terrorism Risk Assessment
- —— 8 —— Public Health Policy: Mathematical Formulation of Health Impact Assessments and Multi-Criteria Decision Analysis
- —— 9 —— Environmental Impact Studies: Mathematical Formulation of Life Cycle Assessment and Cumulative Risk Assessment
- —— 10 —— Financial Risk Modeling and Portfolio Optimization: Mathematical Formulation of Market Dynamics and Risk Analysis
- Write an essay on the commonalities among these ten complex systems and the cross-domain insights.
- Quiz
- Provide 25 discussion questions relevant to the content above.








Leave a comment